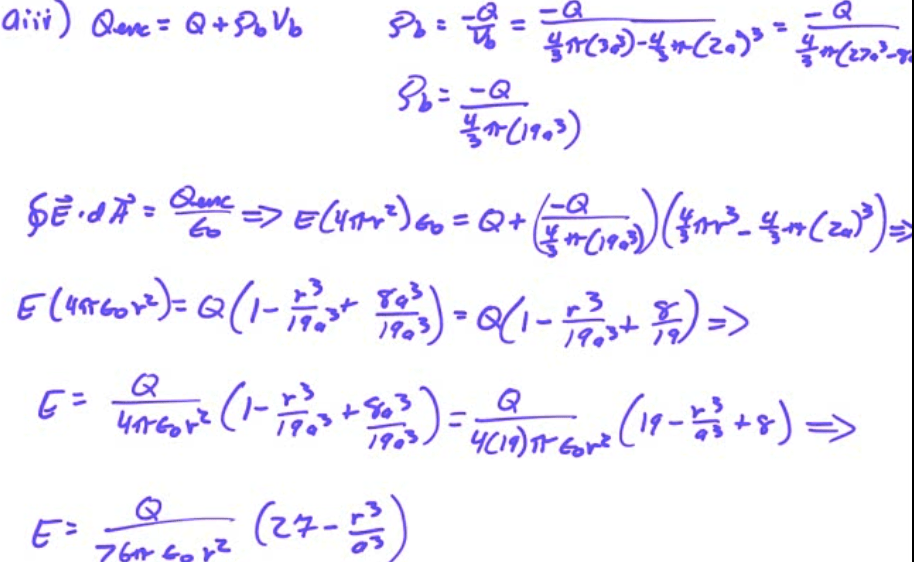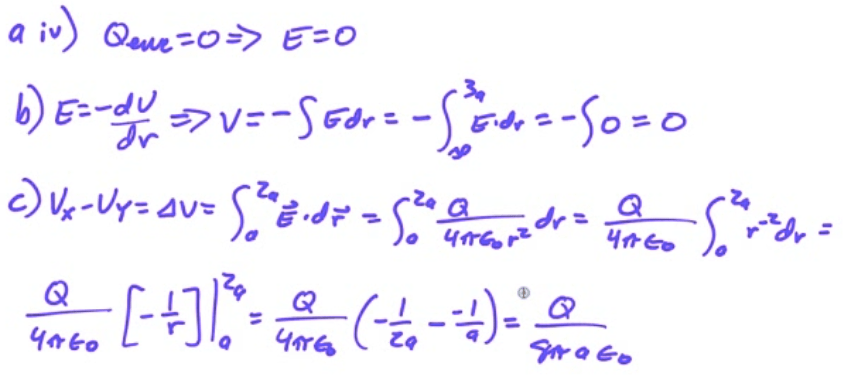Potential Due to a Charged Ring

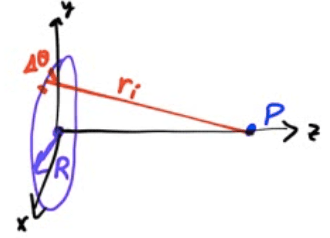
C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image120.png

  • Find the electric potential on the axis of a uniformly charged ring of radius R and total charge Q at point P located a distance z from the center of the ring

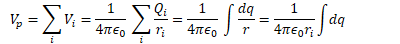
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image121.png

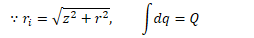
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image122.png

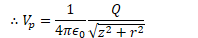
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image123.png

Potential Due to a Charged Disk

aa

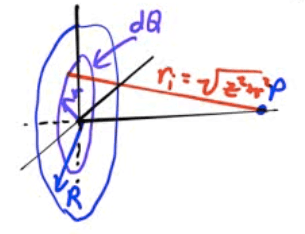
  • Find the electric potential on the axis of a uniformly charged disk of radius R and total charge Q at point P located a distance z from the center of the ring

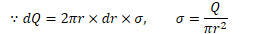
    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image125.png

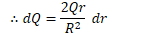
    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image126.png

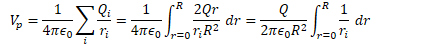
    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image127.png

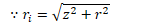
    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image128.png

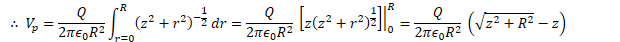
    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image129.png

Potential Due to a Spherical Shell of Charge

C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image130.png

  • Find the electric potential both inside and outside a uniformly charged shell of radius R and total charge Q

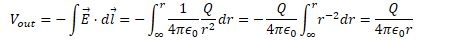
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image131.png

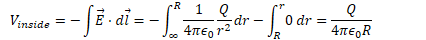
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image132.png

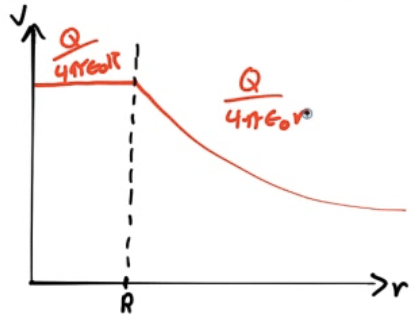
    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image133.png

Potential Due to a Uniform Solid Sphere

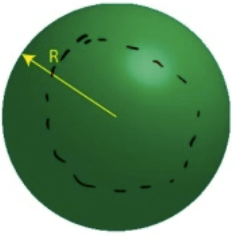
C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image134.png

  • Find the electric field and electric potential inside a uniformly charged solid insulating sphere of radius R and total charge Q

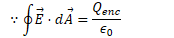
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image135.png

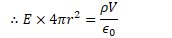
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image136.png

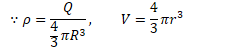
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image137.png

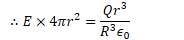
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image138.png

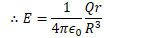
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image139.png

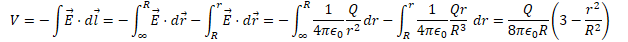
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image140.png

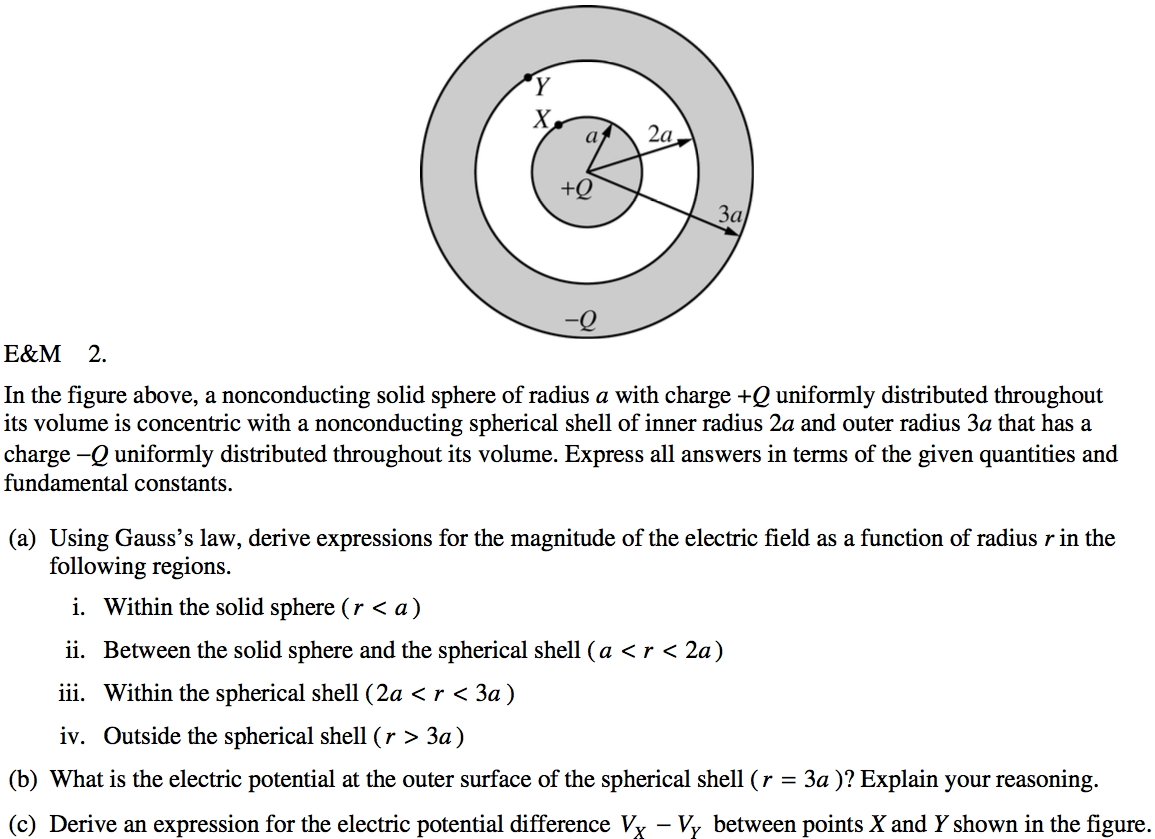
2012 Free Response Question 1

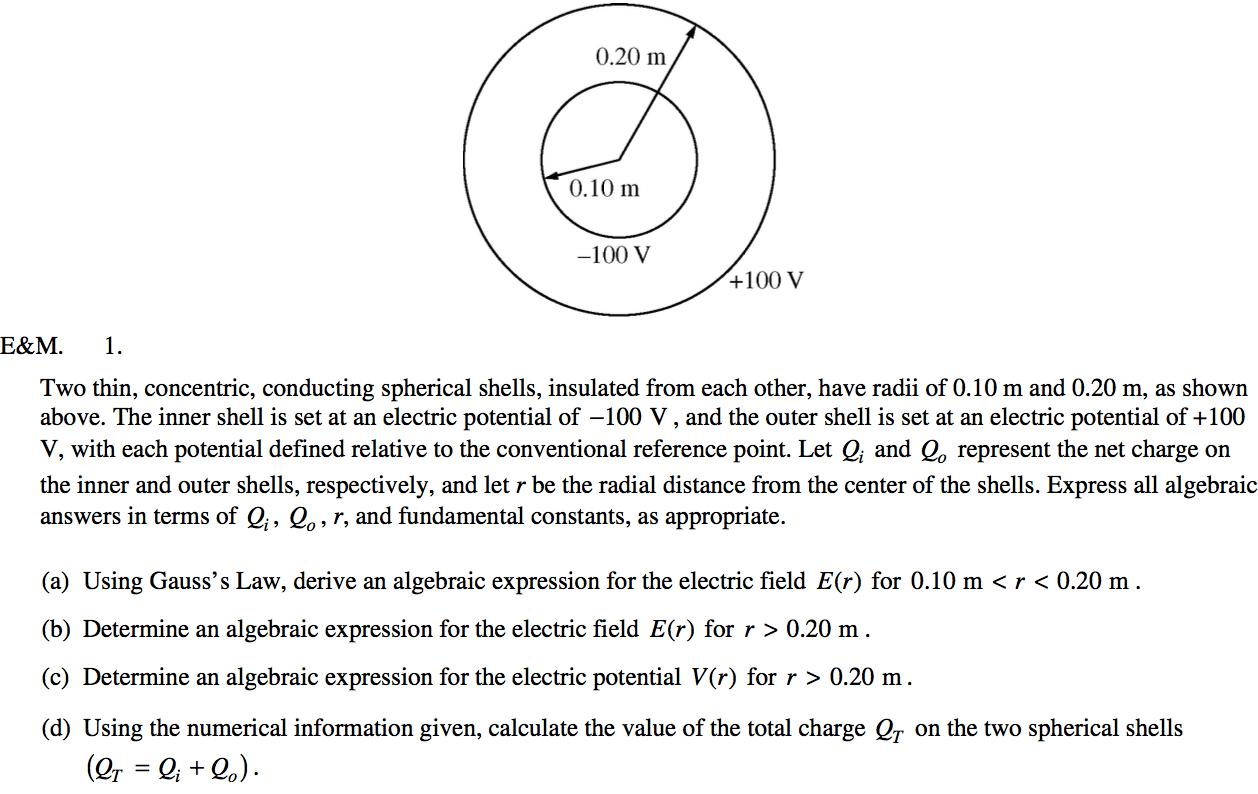
0.20 m 0.10 m -100 v +100 V Two thin, concentric, conducting spherical shells, insulated from each other, have radii of 0.10 m and 0.20 m, as shown above. The inner shell is set at an electric potential of —100 V , and the outer shell is set at an electric potential of +100 V, with each potential defined relative to the conventional reference point. Let Q and Q represent the net charge on the inner and outer shells, respectively, and let r be the radial distance from the center of the shells. Express all algebraic answers in terms of Q, Qo , r, and fundamental constants, as appropriate. (a) Using Gauss's Law, derive an algebraic expression for the electric field E(r) for 0.10 m < r < 0.20 m . (b) Determine an algebraic expression for the electric field E(r) for r > 0.20 m . (c) Determine an algebraic expression for the electric potential V(r) for r > 0.20 m . (d) Using the numerical information given, calculate the value of the total charge QT on the two spherical shells (QT =Q+QO).

(e) On the axes below, sketch the electric field E as a function of r . Let the positive direction be radially outward. o. 10 0.20 (f) On the axes below, sketch the electric potential V as a function of r . o. 10 0.20 0.30 0.30

nootzn اد ٩2 ادده(oبe( مء«دمم م ديه « (همك. (مصن -- ددمى ما (-)ـ -(■:-صم ابي ذ" - ٠ ٣٩ م-ـ ي) ه ارهه مه هيم - ره ميه دي إوهام قداس. يحة ؤو.»لا، م وو ود«ن. وو.»لاء (ادمو

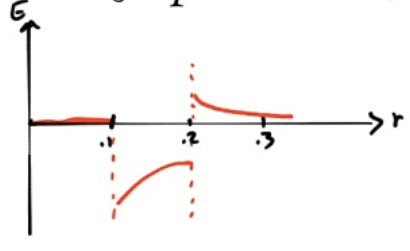
C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image144.png

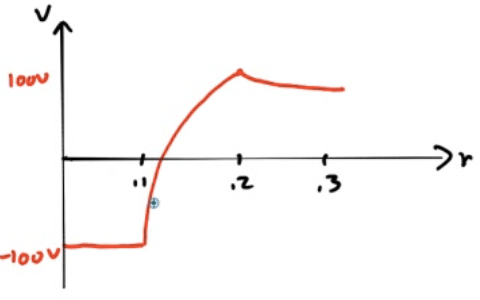
C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image145.png

2010 Free Response Question 1

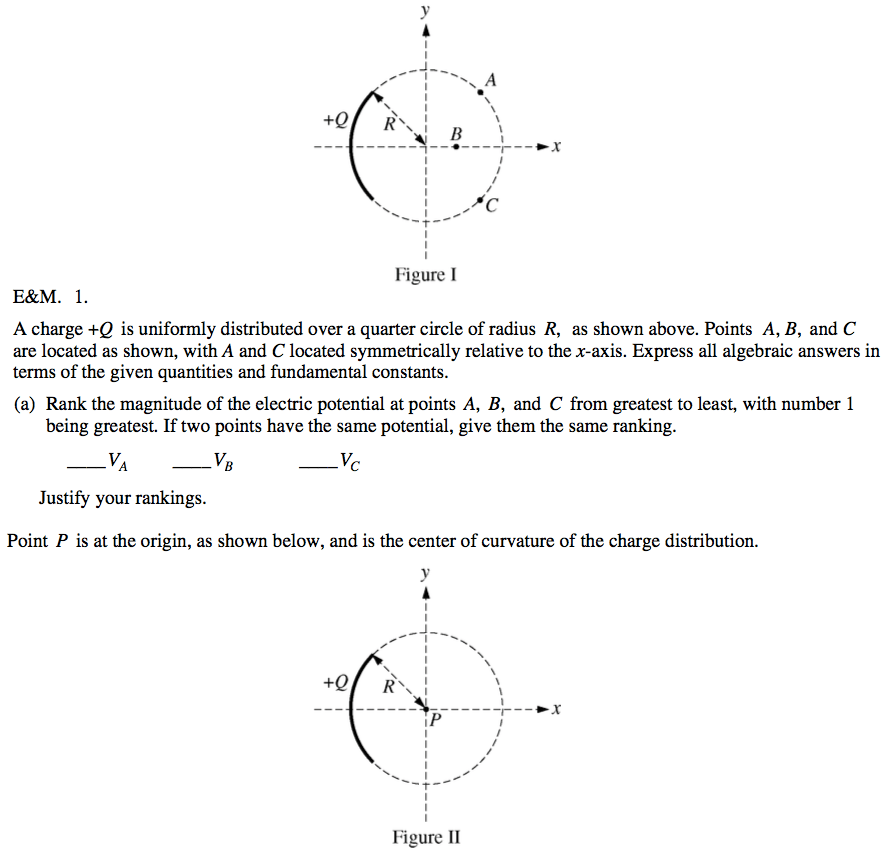
+Q E\&M. 1. Figure I A charge +Q is uniformly distributed over a quarter circle of radius R, as shown above. Points A, B, and C are located as shown, with A and C located symmetrically relative to the x-axis. Express all algebraic answers in terms of the given quantities and fundamental constants. (a) Rank the magnitude of the electric potential at points A, B, and C from greatest to least, with number 1 being greatest. If two points have the same potential, give them the same ranking. Justify your rankings. Point P is at the origin, as shown below, and is the center of curvature of the charge distribution. +Q Figure Il

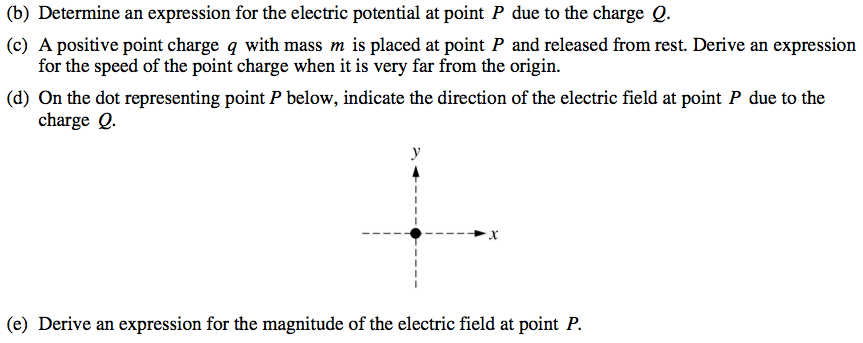
(b) (c) (d) (e) Determine an expression for the electric potential at point P due to the charge Q. A positive point charge q with mass m is placed at point P and released from rest. Derive an expression for the speed of the point charge when it is very far from the origin. On the dot representing point P below, indicate the direction of the electric field at point P due to the charge Q. -9 Derive an expression for the magnitude of the electric field at point P.

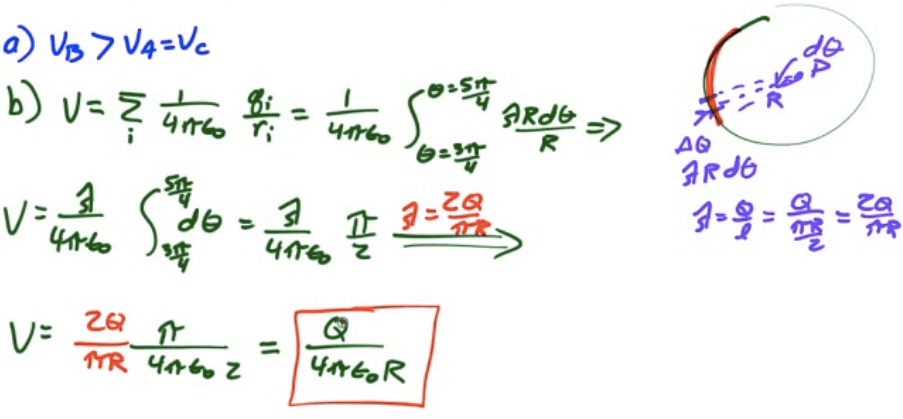
C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image148.png

C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image149.png

2009 Free Response Question 1

![A spherically symmetric charge distribution has net positive charge Q) distributed within a radius of R. Its electric potential V as a function of the distance r from the center of the sphere is given by the following. V(r) = 2 -2+3 for r < R 41t€0R V(r) = for r > R 41t€or Express all algebraic answers in terms of the given quantities and fundamental constants. (a) For the following regions, indicate the direction of the electric field E(r) and derive an expression for its magnitude. Radially inward ii. r > R Radially inward Radially outward Radially outward (b) For the following regions, derive an expression for the enclosed charge that generates the electric field in that region, expressed as a function of r. ii. r

R (c) Is there any charge on the surface of the sphere (r = R) ? Yes No If there is, determine the charge. In either case, explain your reasoning. ](./media/image150.png)

(d) On the axes below, sketch a graph of the force that would act on a positive test charge in the regions r < R and r > R. Assume that a force directed radially outward is positive.

C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image152.png

C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image153.png

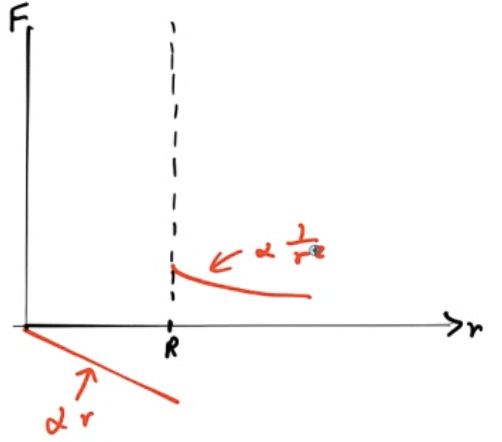
C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image154.png

2007 Free Response Question 2

-Q In the figure above, a nonconducting solid sphere of radius a with charge +Q uniformly distributed throughout its volume is concentric with a nonconducting spherical shell of inner radius 2a and outer radius 3a that has a charge —Q uniformly distributed throughout its volume. Express all answers in terms of the given quantities and fundamental constants. (a) Using Gauss's law, derive expressions for the magnitude of the electric field as a function of radius rin the following regions. i. Within the solid sphere (r < a) ii. Between the solid sphere and the spherical shell (a < r < 2a) iii. Within the spherical shell (2a < r < 3a ) iv. Outside the spherical shell (r > 3a) (b) What is the electric potential at the outer surface of the spherical shell ( r = 3a )? Explain your reasoning. (c) Derive an expression for the electric potential difference Vx — VY between points X and Y shown in the figure.

3Q

C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image157.png

C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image158.png

results matching ""

    No results matching ""